Table of Contents
工作量證明 POW
工作量證明本質上是一個區塊中的交易被驗證的過程,只要礦工按照要求完成了工作量證明,並且區塊中的交易確認為有效,那麼整個區塊就會被添加到區塊鏈中。一般我們也可以這樣理解,工作量證明的成果是一串有效的數據,它的生成無論在時間、複雜性還是支出方面都具有難度。而當這個數據生成之後,網絡上的其他用戶能夠相對容易地進行讀取、識別和驗證。在比特幣區塊鏈中,工作量證明的有效成果就是找到每個新區塊被賦予的哈希值。
簡單來說 工作量證明就是一份證明,用來確認你做過一定量的工作。
監測工作的整個過程通常是極為低效的,而通過對工作的結果進行認證來證明完成了相應的工作量,則是一種非常高效的方式。Ex : 畢業證、駕駛證。也是通過檢驗結果的方式(相關的考試)所取得的證明
工作量證明系統
工作量證明系統(或者說協議、函數),是一種應對拒絕服務攻擊和其他服務濫用的經濟對策。它要求發起者進行一定量的運算,也就意味著需要消耗計算機一定的時間。這個概念由Cynthia Dwork 和Moni Naor 1993年在學術論文中首次提出。
工作量證明(POW)這個名詞,則是在1999年Markus Jakobsson 和Ari Juels的文章中才被真正提出。哈希現金是一種工作量證明機制,它是亞當·貝克(Adam Back)在1997年發明的,用於抵抗郵件的拒絕服務攻擊及垃圾郵件網關濫用。在比特幣之前,哈希現金被用於垃圾郵件的過濾,也被微軟用於hotmail/exchange/outlook等產品中(微軟使用一種與哈希現金不兼容的格式並將之命名為電子郵戳)。
哈希現金也被哈爾·芬尼以可重複使用的工作量證明(RPOW)的形式用於一種比特幣之前的加密貨幣實驗中。另外,戴偉的B-money、尼克·薩博的比特金(Bit-Gold)這些比特幣的先行者,都是在哈希現金的框架下進行挖礦的。
哈希函數(Hash Function)
哈希函數(也稱為散列函數),給定一個輸入x,它會算出相應的輸出H(x)。
哈希函數的主要特徵是:
1.輸入x可以是任意長度的字符串
2.輸出結果即H(x)的長度是固定的
3.計算H(x)的過程是高效的(對於長度為n的字符串x,計算出H(x)的時間複雜度應為O(n))
而對於比特幣這種加密系統所使用的哈希函數,它需要另外具備以下的性質:
- 免碰撞,即不會出現輸入x≠y,但是H(x)=H(y)
其實這個特點在理論上並不成立,比如,比特幣使用的SHA256算法,會有2^256種輸出,如果我們進行2^256+1次輸入,那麼必然會產生一次碰撞;甚至從概率的角度看,進行2^130次輸入就會有99%的可能發生一次碰撞。不過我們可以計算一下,假設一台計算機以每秒10000次的速度進行哈希運算,要經過10^27年才能完成2^128次哈希!甚至可以這麼說,即便是人類製造的所有計算機自宇宙誕生開始一直運算到今天,發現碰撞的機率也是極其小的。
2. 隱匿性,也就是說,對於一個給定的輸出結果H(x),想要逆推出輸入x,在計算上是不可能的。
3. 不存在比窮舉更好的方法,可以使哈希結果H(x)落在特定的範圍。
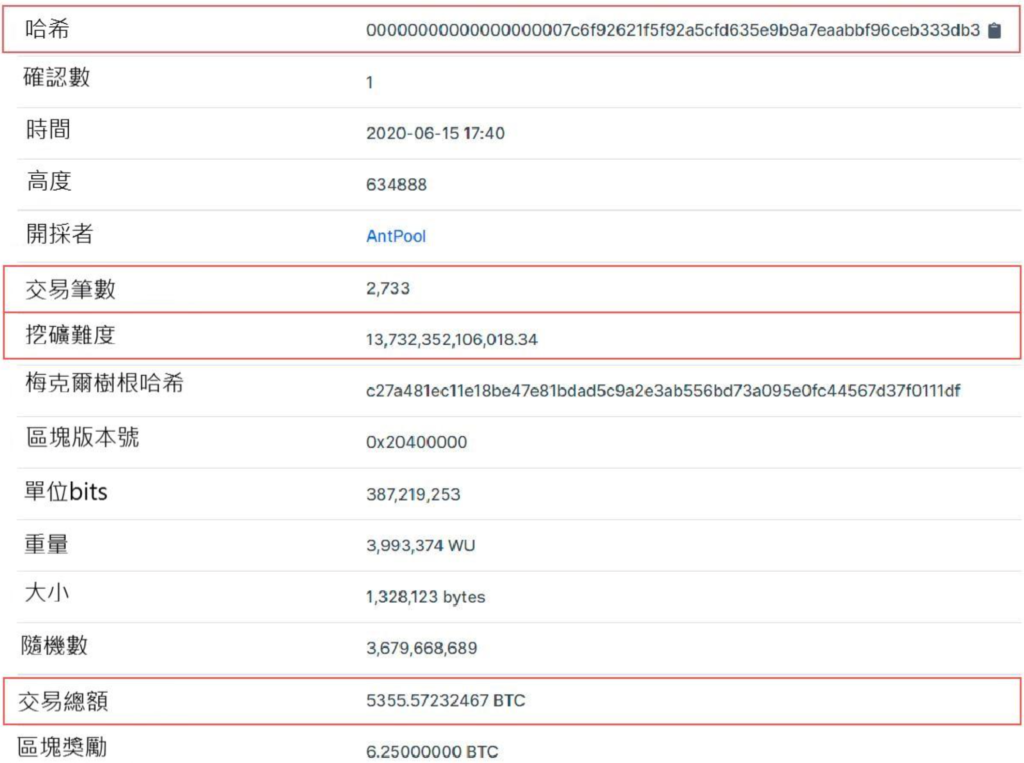
圖來自IG
我們在(一、比特幣是什麼?)中有提到,哈希值是一個區塊中所有數據的總和,這些數據經過運算被轉化成能夠被讀懂且易於區分的代碼。
(一)比特幣 Bitcoin 是什麼?用白話文讓你一次看懂
其他一些比較有趣的指標包括這個區塊中的交易筆數(2733)以及交易總額(5355.57232467 BTC),即該區塊中所有交易綜合起來的比特幣數額。
不過最有趣的指標還是要看挖礦難度,因為它就是工作量證明的工作努力方向。在這個示例中,要第一個算出符合要求哈希值的難度係數是13732253106018(或接近14萬億)。在這種難度級別下,傳統的電腦幾乎不可能率先算出有效的哈希值,這也是礦工經常將他們的資源集中在一起以最大限度地提高成功機會的原因。
工作證明原理
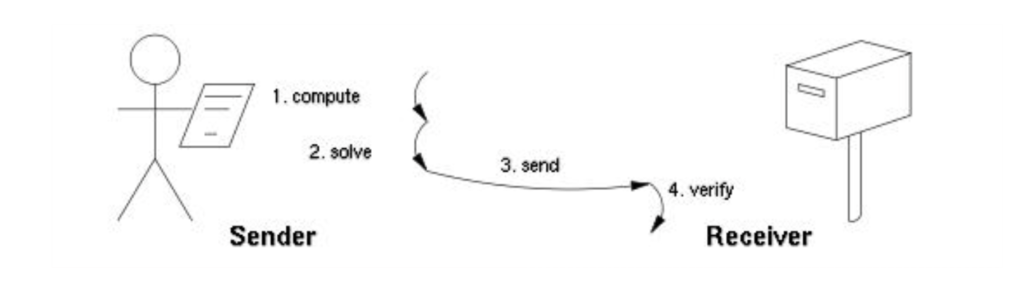
工作量證明系統主要特徵是客戶端需要做一定難度的工作得出一個結果,驗證方卻很容易通過結果來檢查出客戶端是不是做了相應的工作。這種方案的一個核心特徵是不對稱性:工作對於請求方是適中的,對於驗證方則是易於驗證的。它與驗證碼不同,驗證碼的設計出發點是易於被人類解決而不易被計算機解決。
e.g. 我們給定的一個基本的字符串”Hello, world!”,我們給出的工作量要求是,可以在這個字符串後面添加一個叫做nonce的整數值,對變更後(添加nonce)的字符串進行SHA256哈希運算,如果得到的哈希結果(以16進制的形式表示)是以”0000″開頭的,則驗證通過。為了達到這個工作量證明的目標。我們需要不停的遞增nonce值,對得到的新字符串進行SHA256哈希運算。按照這個規則,我們需要經過4251次計算才能找到恰好前4位為0的哈希散列。
比特幣中的工作量證明
比特幣網絡中任何一個節點,如果想生成一個新的區塊並寫入區塊鏈,必須解出比特幣網絡出的工作量證明的迷題。這道題關鍵的三個要素是工作量證明函數、區塊及難度值。工作量證明函數是這道題的計算方法,區塊決定了這道題的輸入數據,難度值決定了這道題的所需要的計算量。
1.工作量證明函數
和我們上節例子中用到的哈希函數一樣,比特幣系統中使用的工作量證明函正是SHA256。
SHA是安全散列算法(Secure Hash Algorithm)的縮寫,是一個密碼散列函數家族。這一組函數是由美國國家安全局(NSA)設計,美國國家標準與技術研究院(NIST) 發布的,主要適用於數字簽名標準。SHA256就是這個函數家族中的一個,是輸出值為256位的哈希算法。到目前為止,還沒有出現對SHA256算法的有效攻擊。
2.區塊

比特幣的區塊由區塊頭及該區塊所包含的交易列表組成。區塊頭的大小為80字節,由4字節的版本號、32字節的上一個區塊的散列值、32字節的Merkle Root Hash、4字節的時間綴(當前時間)、4字節的當前難度值、4字節的隨機數組成。區塊包含的交易列表則附加在區塊頭後面,其中的第一筆交易是coinbase交易,這是一筆為了讓礦工獲得獎勵及手續費的特殊交易。
擁有80字節固定長度的區塊頭,就是用於比特幣工作量證明的輸入字符串。因此,為了使區塊頭能體現區塊所包含的所有交易,在區塊的構造過程中,需要將該區塊要包含的交易列表,通過Merkle Tree算法生成Merkle Root Hash,並以此作為交易列表的摘要存到區塊頭中。
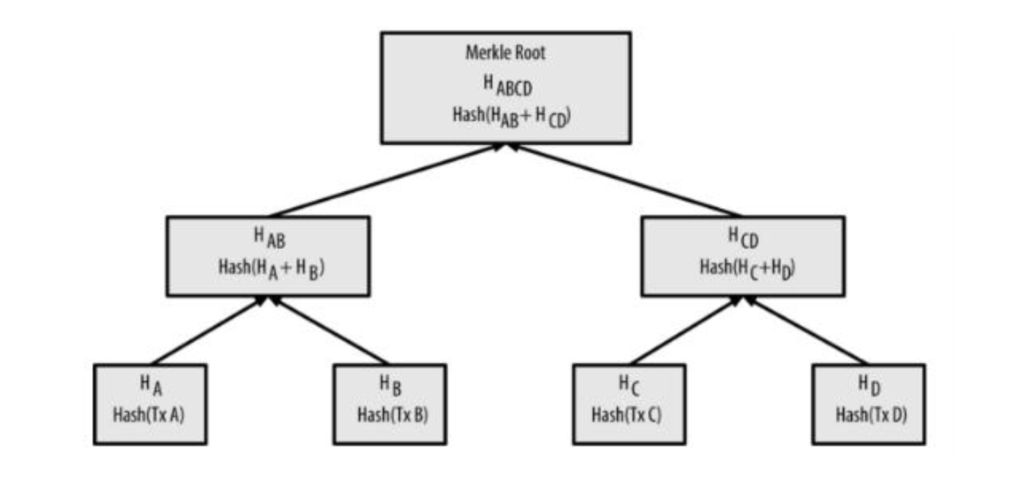
Merkle Tree的算法圖解
3.難度值
難度值(difficulty)是礦工們在挖礦時候的重要參考指標,它決定了礦工大約需要經過多少次哈希運算才能產生一個合法的區塊。比特幣的區塊大約每10分鐘生成一個,如果要在不同的全網算力條件下,新區塊的產生保持都基本這個速率,難度值必鬚根據全網算力的變化進行調整。簡單地說,難度值被設定在無論挖礦能力如何,新區塊產生速率都保持在10分鐘一個。
難度的調整是在每個完整節點中獨立自動發生的。每2016個區塊,所有節點都會按統一的公式自動調整難度,這個公式是由最新2016個區塊的花費時長與期望時長(期望時長為20160分鐘即兩週,是按每10分鐘一個區塊的產生速率計算出的總時長)比較得出的,根據實際時長與期望時長的比值,進行相應調整(或變難或變易)。也就是說,如果區塊產生的速率比10分鐘快則增加難度,比10分鐘慢則降低難度。
這個公式可以總結為如下形式:
新難度值= 舊難度值* ( 過去2016個區塊花費時長/ 20160 分鐘 )
工作量證明需要有一個目標值。比特幣工作量證明的目標值(Target)的計算公式如下:
目標值= 最大目標值/ 難度值
其中最大目標值為一個恆定值:
0x00000000FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF
目標值的大小與難度值成反比。比特幣工作量證明的達成就是礦工計算出來的區塊哈希值必須小於目標值。
與第3節所舉的例子相類比,我們也可以簡單理解成,比特幣工作量證明的過程,就是通過不停的變換區塊頭(即嘗試不同的nouce值)作為輸入進行SHA256哈希運算,找出一個特定格式哈希值的過程(即要求有一定數量的前導0)。而要求的前導0的個數越多,代表難度越大。
4.工作量證明的過程

我們可以把比特幣礦工解這道工作量證明迷題的步驟大致歸納如下:
生成Coinbase交易,並與其他所有準備打包進區塊的交易組成交易列表,通過Merkle Tree算法生成Merkle Root Hash
把Merkle Root Hash及其他相關字段組裝成區塊頭,將區塊頭的80字節數據(Block Header)作為工作量證明的輸入
不停的變更區塊頭中的隨機數即nonce的數值,並對每次變更後的的區塊頭做雙重SHA256運算(即SHA256(SHA256(Block_Header))),將結果值與當前網絡的目標值做對比,如果小於目標值,則解題成功,工作量證明完成。
比特幣的工作量證明,就是我們俗稱“挖礦”所做的主要工作。理解工作量證明機制,將為我們進一步理解比特幣區塊鏈的共識機制奠定基礎。
關於工作量證明的詳細說明,因沒有太多資料,所以主要來自原文網誌

